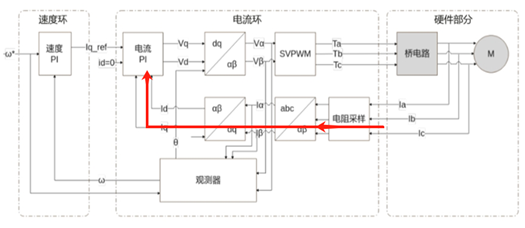
上一章節(jié)我們了解完無感 FOC 的整個(gè)流程和原理，我們都知道，要想估算出轉(zhuǎn)字的實(shí)際轉(zhuǎn)速和角度，我們就必須要先要采集三相電流 IA、IB、IC，再通過 Clark 變化、Park 變化和反 Park 變換。上一章已經(jīng)為大家介紹了單電阻采樣、雙電阻采樣和三電阻采樣，這節(jié)將為大家介紹 Clark 變換、Park 變換和反 Park 變換。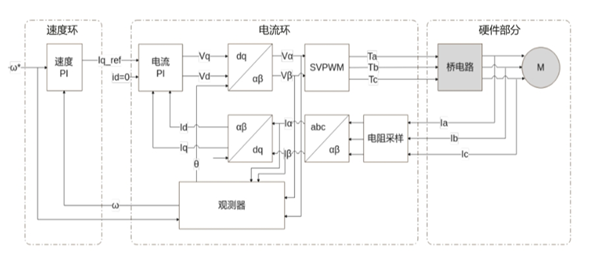
       

在介紹之前，我們需要先了解電機(jī)控制其實(shí)控制的不是電流，控制的是轉(zhuǎn)矩，而電機(jī)的轉(zhuǎn)矩是磁場作用后的結(jié)果。在直流電機(jī)中，定子動子的磁場方向是固定不變的，所以只需要調(diào)節(jié)電流就能達(dá)到調(diào)節(jié)轉(zhuǎn)矩的效果，但是交流電機(jī)的轉(zhuǎn)矩是幅值、角度的函數(shù)，是一個(gè)非線性系統(tǒng)。但是控制非線性系統(tǒng)是很難得到一個(gè)好的動態(tài)響應(yīng)的，但是如果能把幅值和角度進(jìn)行分解，把非線性系統(tǒng)轉(zhuǎn)化成線性系統(tǒng)來控制，或者說把交流電機(jī)當(dāng)作直流電機(jī)來控制的話，就能通過 PI控制得到優(yōu)秀的動態(tài)控制性能，而 Clark 變換和 Park 變換正式起到了這個(gè)作用，除此之外，將三相電流變換到兩相靜止坐標(biāo)系下后，還減少了運(yùn)算量。

        簡單來說，就是因?yàn)橥ㄟ^了 Clark 變換、Park 變換可以將三相交流的電信號轉(zhuǎn)換成直流信號，再通過 PI 控制該直流電流，模擬直流電機(jī)的控制方式，以達(dá)到穩(wěn)定控制交流電機(jī)的效果。

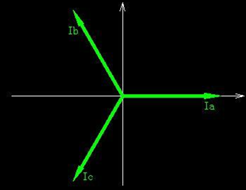
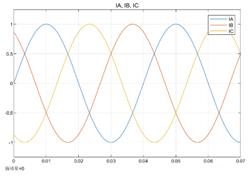
        前面為大家講過，三相電流的 Ia，Ib，Ic 可根據(jù)基爾霍夫定律得 Ia + Ib + Ic = 0，并且三相電流的相位差如下圖所示：

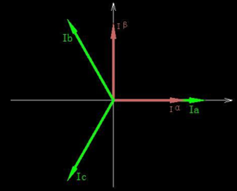
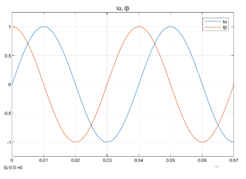
        圖中 Ia、Ib、Ic 分別是三相電流，經(jīng)過 Clark 變換我們可以將三相靜止坐標(biāo)系里面的向量變換到兩相靜止坐標(biāo)系，以得到Iα, Iβ，α 軸的方向與電機(jī)A 相方向相同，β 軸垂直于α 軸。

         →       

       Clark 變換公式如下：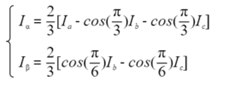

       我們可以看到，變換后的波形仍然是正弦波，但是我們要控制的變量少了一個(gè)。如下圖所示：

    →      

       但是我們可以看到，現(xiàn)在被控制的量仍然是兩個(gè)非線性的量，不適合 PID 線性調(diào)制器，因此我們要將其線性化，此時(shí) Park 變換就登場了！！

       Park 變換是將兩相靜止坐標(biāo)系轉(zhuǎn)換成兩相旋轉(zhuǎn)坐標(biāo)系，對應(yīng)是的將 α-β 轉(zhuǎn)成d-q，它會隨著電機(jī)的轉(zhuǎn)子不停旋轉(zhuǎn)，我們以轉(zhuǎn)子的磁場方向（轉(zhuǎn)子 N 極方向）為 d 軸正方向，以垂直于轉(zhuǎn)子磁場的方向?yàn)閝 軸方向，旋轉(zhuǎn)坐標(biāo)系 d-q 與兩相靜止坐標(biāo)系 α-β 的夾角是 θ。

       Park 變換公式如下：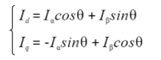

       經(jīng)過 Park 變換后，需要控制的量都被線性化了，這樣的話，我們原來需要控制的三個(gè)非線性的量，就被簡化成了兩個(gè)線性的量：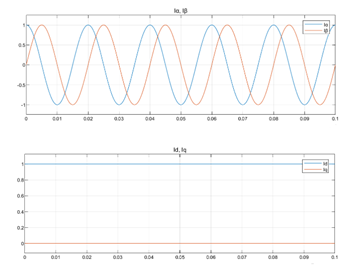

       這樣我們就可以通過調(diào)整 Ud 和 Uq ，從而獲得我們想要的 Id_ref、Iq_ref 值，也就是經(jīng)過了下面的流程：

       在計(jì)算完后，需要經(jīng)過反 Park 變換，將 d-q 坐標(biāo)系轉(zhuǎn)回α-β 坐標(biāo)系，Park 逆變換的公式如下：

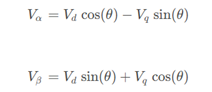
       但是大家看到反 Park 變換的下一步是 SVPWM，以得出能作用在電機(jī)三相上的相電壓 Ua、Ub、Uc，那為什么用的不是 Clark 變換呢？在解答這個(gè)問題之前，我們要先區(qū)分三個(gè)概念：端電壓、線電壓、相電壓。

       端電壓：端電壓就是電機(jī)三相線端相對于GND的電壓，A相端電壓記作UA，B相端電壓記作UB，C相端電壓記作UC;

       線電壓：線電壓就是相相之間的電壓Uab = UA - UB，Ubc = ...;

       相電壓：相電壓就是電機(jī)三相線端相對于連接點(diǎn)N的電壓，UAN = UA - UN，UBN = ...;

       我們可以看出，如果要控制電機(jī)的話，我們需要得到的是三相電壓 UAN、UBN 和 UCN，但是我們通過逆變電路只能控制三相的端電壓，而不能控制三相的相電壓，是無法實(shí)現(xiàn)對電機(jī)的控制的。所以最后一步用的不是反 Clark 變換而是 SVPWM（空間矢量脈寬調(diào)制）。

       那 SVPWM 是怎么得出三相的相電壓呢？結(jié)合上一章我們知道通過定義上橋臂的開關(guān)管導(dǎo)通時(shí)為“1”，關(guān)斷時(shí)為“0”，這樣可以得出六組基本非零矢量 V001、V010、V011、V100、V101、V110 和兩組零矢量 V000、V111。又因?yàn)槿�相星型電機(jī)一般都是對稱繞組，相電阻一樣，以 V4（100）為例子，簡化上面的圖后得到用R 代表三相繞組的阻抗：

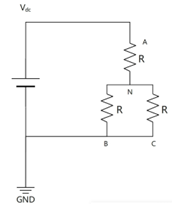
          根據(jù)分壓的原理可以得出下面結(jié)論：

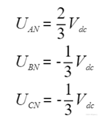
          八種矢量的相電壓推導(dǎo)完后，可以得出如下的表格：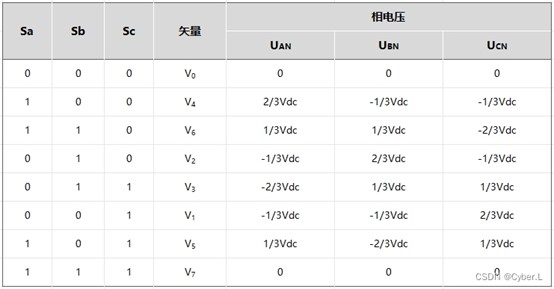

         好啦，今天為大家簡單介紹了 Clark 變換、Park 變換和反 Park 變換，下一章將帶大家介紹觀測器的分類和作用。